
参考资料:
因为最近一直在学数据库和处理病例数据的相关的东西,病例数据嘛,有缺失值太正常了。同时,也因为写的是实际碰到问题的时候找解决办法用的记录,所以都偏向实战而非理论。这篇博文主要针对连续型数据缺失值,其他类型数据可能还需要仔细看文档。
以往碰到的数据缺失值都不是很多,所以对于缺失值的处理都比较简单粗暴——先用 Amelia::missmap() 简单看下大概没问题之后, complete.case() 一把梭哈。但是这次实际处理病例数据发现,病例数据本来算是比较宝贵的的,随便 complete.case() 损失很多信息。并且当然文献里也都是用 mean/median 之类来代替这样,所以就觉得好好研究下怎么来处理缺失值。
MICE
先来看大名鼎鼎的 MICE 包,这个包全名就叫“Multivariate Imputation by Chained Equations”,从名字和介绍就可以看出来人家就是为处理各种类型的数据里的缺失值的:
Multiple imputation using Fully Conditional Specification (FCS) implemented by the MICE algorithm as described in Van Buuren and Groothuis-Oudshoorn (2011) doi:10.18637/jss.v045.i03. Each variable has its own imputation model. Built-in imputation models are provided for continuous data (predictive mean matching, normal), binary data (logistic regression), unordered categorical data (polytomous logistic regression) and ordered categorical data (proportional odds). MICE can also impute continuous two-level data (normal model, pan, second-level variables). Passive imputation can be used to maintain consistency between variables. Various diagnostic plots are available to inspect the quality of the imputations.
缺失值总体来说分为两类:
- MAR: Missing at random. 随机缺失。这一般也是也是我们希望的理想情况。
- MNAR: Missing NOT at random. 非随机缺失。
非随机就比较麻烦了,数据不是随机缺失的处理缺失值当然更容易不准。但是就算数据是随机缺失,缺失值太多肯定也不太好。一般来说,约定俗成的认为 5% 以内的缺失值可以接受。如果哪个变量或者观测的缺失超过 5% 了我们可能就需要考虑要不要把这个变量或者把缺失值的观测删掉了。
MICE 假定数据缺失是 MAR,随机缺失意味着某个值缺失的可能性是依赖于其他的值的,所以也就可以通过其他的值来预测这个缺失的值了。MICE 对缺失值的模拟是通过对一个一个变量的模拟模型进行的。比如我们有 X1、X2 … Xk 一个 k 个变量。如果 X1 有缺失值,那就用剩下的 X2 ~ Xk 变量对 X1 进行回归,X1 的缺失值的模拟值就用回归的结果来代替。依此类推,只要哪个变量有缺失值就用剩余其他变量来回归模拟缺失值进行填补。
默认情况下,对连续性数据的模拟采用线性回归,分类变量就用逻辑回归。所以模拟完成的时候,我们得到一系列的数据,并且这些数据的不同仅仅在于模拟填补的缺失值部分。一般来说,后面最好对这些数据分开建模然后合并结果。MICE 包用到的方法有:
- PMM (Predictive Mean Matching) – 数值型变量
- logreg (Logistic Regression) – 二分类变量
- polyreg (Bayesian polytomous regression) – 类别超过 2 的分类变量
- Proportional odds model - 有序的分类变量
下面我们就应 MICE 和一个随机添加了缺失值的 iris 数据作为实例来看 MICE 是怎么用的。
1
2
3
4
5
6
7
8
9
10
11
12
|
library(mice)
library(missForest)
data(iris)
summary(iris)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
Min. :4.300 Min. :2.000 Min. :1.000 Min. :0.100 setosa :50
1 st Qu.:5.100 1 st Qu.:2.800 1 st Qu.:1.600 1 st Qu.:0.300 versicolor:50
Median :5.800 Median :3.000 Median :4.350 Median :1.300 virginica :50
Mean :5.843 Mean :3.057 Mean :3.758 Mean :1.199
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
|
然后我们随机在数据里产生 10% 的 缺失值。同时,这里我们先来看连续型数据缺失值的处理,所以我们把 Species 这个分类变量也去掉了。
1
2
3
4
5
6
7
8
9
10
11
12
|
set.seed(1234)
iris.mis <- missForest::prodNA(iris, noNA = 0.1) %>%
select(-Species)
summary(iris.mis)
Sepal.Length Sepal.Width Petal.Length Petal.Width
Min. :4.300 Min. :2.200 Min. :1.000 Min. :0.100
1 st Qu.:5.100 1 st Qu.:2.800 1 st Qu.:1.600 1 st Qu.:0.300
Median :5.800 Median :3.000 Median :4.400 Median :1.300
Mean :5.854 Mean :3.063 Mean :3.773 Mean :1.219
3rd Qu.:6.400 3rd Qu.:3.300 3rd Qu.:5.100 3rd Qu.:1.800
Max. :7.900 Max. :4.400 Max. :6.900 Max. :2.500
NA's :16 NA's :16 NA's :14 NA's :18
|
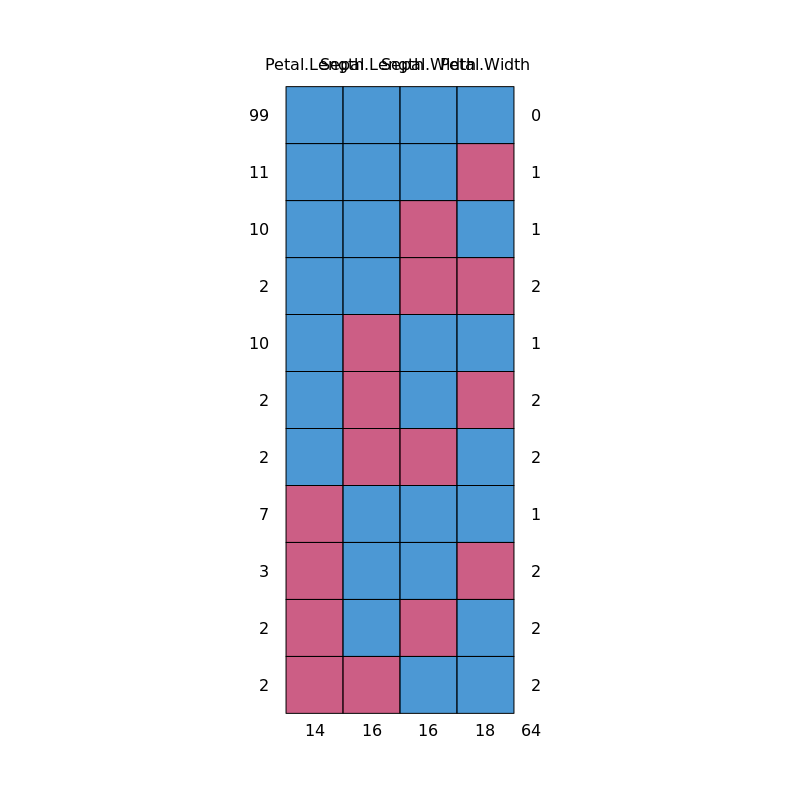
MICE 也提供了可视化缺失值的函数 md.pattern():
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
md.pattern(iris.mis)
Petal.Length Sepal.Length Sepal.Width Petal.Width
99 1 1 1 1 0
11 1 1 1 0 1
10 1 1 0 1 1
2 1 1 0 0 2
10 1 0 1 1 1
2 1 0 1 0 2
2 1 0 0 1 2
7 0 1 1 1 1
3 0 1 1 0 2
2 0 1 0 1 2
2 0 0 1 1 2
14 16 16 18 64
|
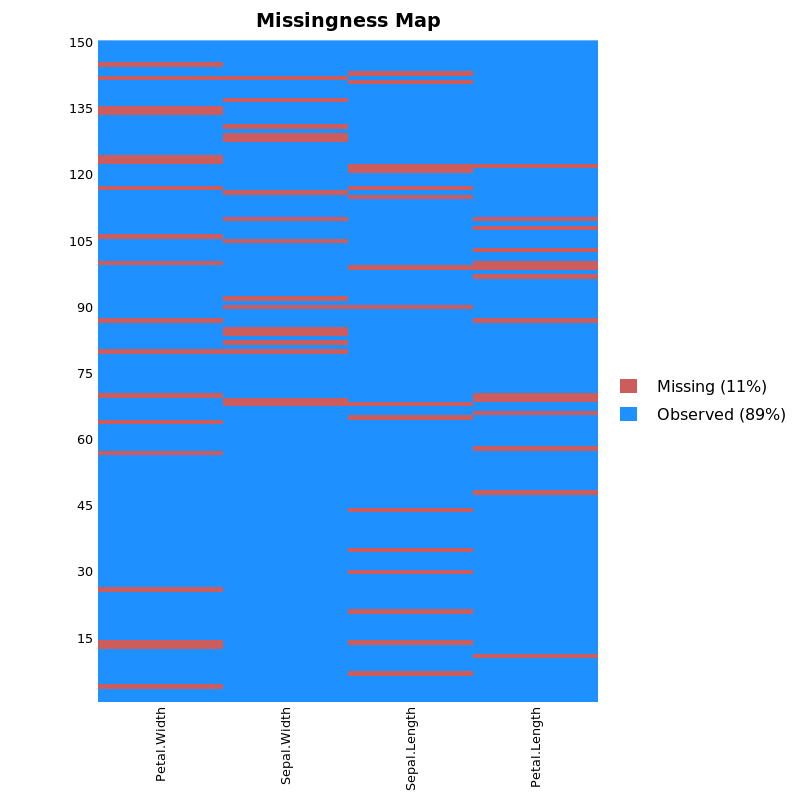
或者 Amelia 的 missmap() 其实更加直观一点,当然没有那么多信息:
1
|
Amelia::missmap(iris.mis)
|
下面我们就可以开始模拟填补缺失值了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
imputed_Data <- mice(iris.mis, m=5, maxit = 50, method = 'pmm', seed = 123)
summary(imputed_Data)
Class: mids
Number of multiple imputations: 5
Imputation methods:
Sepal.Length Sepal.Width Petal.Length Petal.Width
"pmm" "pmm" "pmm" "pmm"
PredictorMatrix:
Sepal.Length Sepal.Width Petal.Length Petal.Width
Sepal.Length 0 1 1 1
Sepal.Width 1 0 1 1
Petal.Length 1 1 0 1
Petal.Width 1 1 1 0
|
上面的代码的意思是:
- m = 5 ,表示生成 5 个填补好的数据
- maxit = 50,每次产生填补数据的迭代次数,这里取 50 次
- method = ‘pmm’,上面介绍的连续型数据采用 Predictive Mean Matching 的方法
来看看我们刚刚生成的 Sepal.Width 值:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
|
imputed_Data$imp$Sepal.Width
1 2 3 4 5
9 3.1 3.0 3.3 3.3 2.8
14 3.0 3.2 3.0 3.0 3.3
20 3.3 3.0 4.1 3.5 3.7
22 3.3 3.7 3.5 3.5 3.5
23 3.0 3.5 3.4 3.4 3.0
35 3.1 3.0 3.6 3.0 3.2
41 3.4 3.8 3.0 3.1 3.2
46 3.4 3.4 3.4 3.0 3.6
59 3.0 3.1 3.2 3.6 2.8
61 2.8 2.9 3.7 2.6 2.8
66 3.8 3.2 4.1 3.3 3.0
67 2.8 2.3 2.4 2.8 2.7
69 3.8 3.1 2.3 2.6 3.4
71 2.7 3.8 2.8 2.5 2.7
82 2.7 3.0 2.9 2.9 3.2
83 2.8 3.2 2.8 2.9 3.4
dim(imputed_Data$imp$Sepal.Width)
[1] 16 5
|
我们一共生成了 5 组数据,前面我们看到 Sepal.Width 里有 16 个 NA,所以这里我们就得到一个 16 * 5 的数据。
或者我们只想要生成数据里的某一个:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
|
# get complete data ( 2nd out of 5)
completeData.2 <- mice::complete(imputed_Data,2)
sum(is.na(completeData.2))
[1] 0
head(completeData.2)
Sepal.Length Sepal.Width Petal.Length Petal.Width
1 5.1 3.5 1.4 0.2
2 4.9 3.0 1.4 0.2
3 4.7 3.2 1.3 0.2
4 4.6 3.1 1.5 0.2
5 5.0 3.6 1.4 0.2
6 5.4 3.9 1.7 0.2
|
要建模做统计分析的时候,前面也提到,我们可以对每个模型都建模然后合并结果:
1
2
3
4
5
6
7
8
9
10
11
|
# build predictive model
fit <- with(data = imputed_Data, exp = lm(Sepal.Width ~ Sepal.Length + Petal.Width))
# combine results of all 5 models
combine <- pool(fit)
summary(combine)
estimate std.error statistic df p.value
(Intercept) 1.8677059 0.36106651 5.172748 36.47085 8.567029e-06
Sepal.Length 0.3028491 0.07477405 4.050190 33.00981 2.560708e-04
Petal.Width -0.4761426 0.08182634 -5.818941 28.54299 1.160180e-06
|
我们把原始数据的模型和这个对比一下:
1
2
3
4
5
|
summary(lm(Sepal.Width ~ Sepal.Length + Petal.Width, data = iris))
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.92632 0.32094 6.002 1.45e-08 ***
Sepal.Length 0.28929 0.06605 4.380 2.24e-05 ***
Petal.Width -0.46641 0.07175 -6.501 1.17e-09 ***
|
还行,结果还是比较接近的。
其他类型数据
这里简单看一个其他类型数据的处理的例子。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
|
(dat <- read_csv("/path/to/dt_simulated.csv"))
Parsed with column specification:
cols(
Age = col_double(),
Gender = col_character(),
Cholesterol = col_double(),
SystolicBP = col_double(),
BMI = col_double(),
Smoking = col_character(),
Education = col_character()
)
# A tibble: 250 x 7
Age Gender Cholesterol SystolicBP BMI Smoking Education
<dbl> <chr> <dbl> <dbl> <dbl> <chr> <chr>
1 67.9 Female 236. 130. 26.4 Yes High
2 54.8 Female 256. 133. 28.4 No Medium
3 68.4 Male 199. 158. 24.1 Yes High
4 67.9 Male 205 136 19.9 No Low
5 60.9 Male 208. 145. 26.7 No Medium
6 44.9 Female 222. 131. 30.6 No Low
7 49.9 Male 202. 152. 27.3 No Medium
8 55.1 Female 206. 151. 27.5 No Low
9 57.5 Male 202. 142. 28.3 No High
10 77.2 Male 240. 161. 29.1 No High
# ... with 240 more rows
sapply(dat, function(x) sum(is.na(x)))
Age Gender Cholesterol SystolicBP BMI Smoking Education
0 0 0 0 0 0 0
|
(这个数据的是 dt_simulated.csv,但是我在 R 里直接没读进来,大概是网络原因我也懒得去找了。下载到本地自己读的,然后现在也放在这个 GitHub 仓库里了:dt_simulated.csv)
数据一共 205 行 × 7 列,列分别为年龄、性别、胆固醇、血压、BMI、是否抽烟以及教育程度,然后原始数据是没有缺失值的。所以我们先随机的加一些 NA 进去,随后把字符型变量转换成因子:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
original <- dat
set.seed(10)
dat[sample(1:nrow(dat), 5), "Age"] <- NA
dat[sample(1:nrow(dat), 20), "Cholesterol"] <- NA
dat[sample(1:nrow(dat), 5), "BMI"] <- NA
dat[sample(1:nrow(dat), 20), "Smoking"] <- NA
dat[sample(1:nrow(dat), 20), "Education"] <- NA
sapply(dat, function(x) sum(is.na(x)))
Age Gender Cholesterol SystolicBP BMI Smoking Education
5 0 20 0 5 20 20
dat <- dat %>%
mutate(
Smoking = as.factor(Smoking),
Education = as.factor(Education),
Cholesterol = as.numeric(Cholesterol)
)
|
为了自定义 MICE 的整个填补过程,我们先构建一个 mice 对象,然后:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
|
init = mice(dat, maxit=0)
init
Class: mids
Number of multiple imputations: 5
Imputation methods:
Age Gender Cholesterol SystolicBP BMI Smoking Education
"pmm" "" "pmm" "" "pmm" "logreg" "polyreg"
PredictorMatrix:
Age Gender Cholesterol SystolicBP BMI Smoking Education
Age 0 0 1 1 1 1 1
Gender 1 0 1 1 1 1 1
Cholesterol 1 0 0 1 1 1 1
SystolicBP 1 0 1 0 1 1 1
BMI 1 0 1 1 0 1 1
Smoking 1 0 1 1 1 0 1
Number of logged events: 1
it im dep meth out
1 0 0 constant Gender
meth = init$method
meth
Age Gender Cholesterol SystolicBP BMI Smoking Education
"pmm" "" "pmm" "" "pmm" "logreg" "polyreg"
predM = init$predictorMatrix
predM
Age Gender Cholesterol SystolicBP BMI Smoking Education
Age 0 0 1 1 1 1 1
Gender 1 0 1 1 1 1 1
Cholesterol 1 0 0 1 1 1 1
SystolicBP 1 0 1 0 1 1 1
BMI 1 0 1 1 0 1 1
Smoking 1 0 1 1 1 0 1
Education 1 0 1 1 1 1 0
|
可以看到,这个对象里包含了填补缺失值的方法、使用的变量和其他的参数等。我们把 method(用来定义每个变量模拟填补缺失值的方法)和 predictorMatrix(名字就很明显了,用来定义模拟填补每个变量时用到的变量矩阵) 单独取出来了,这样我们就可以模拟过程进行自定义了。
比如有的时候,数据里可能有一列是 ID 值,这时候显然把它用来帮助模拟其他变量的缺失值完全没有意义。以我们这个数据里的 BMI 为例,假设 BMI 是某种编号信息,我们想在预测填补其他变量的缺失值的时候不要使用这种变量,可以 predM[, c("BMI")]=0 把变量矩阵里对应 BMI 这一列全部改成 0,所以矩阵现在就变成预测其他变量的时候不使用 BMI 变量这一列。
但是上面的方法有一个问题,现在给其他变量预测缺失值的时候不会使用 BMI 这一列,但 MICE 仍然会对 BMI 的缺失值进行填补,这显然也没什么意义。meth["BMI"] ="" 会把预测 BMI 时使用的方法变成空值,即不对 BMI 进行预测了。
下面我们把 Age 排除在填补范围外,并且分别针对连续型变量 Cholesterol,二分类变量 Smoke 和有序变量 Education 分别自定义模拟方法,然后进行模式值模拟:
1
2
3
4
5
6
7
8
|
meth[c("Age")] = ""
meth[c("Cholesterol")] = "norm"
meth[c("Smoking")] = "logreg"
meth[c("Education")] = "polyreg"
set.seed(1234)
imputed <- mice(dat, method = meth, predictorMatrix = predM, m = 5)
imputed <- mice::complete(imputed)
|
然后我们检查一下是不是缺失值都没了:
1
2
3
|
sapply(imputed, function(x) sum(is.na(x)))
Age Gender Cholesterol SystolicBP BMI Smoking Education
5 0 0 0 0 0 1
|
Age 里的 5 个缺失值都没有处理,但是 Education 里还剩下一个缺失值也没有处理。似乎与 Age 变量没有处理有关,因为一旦把 Age 的缺失值也处理掉,Education 里全部的缺失值也能得到处理。此处原因待查。
最后我们来看看与原始数据相比,填补缺失值的效果怎么样:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
# Cholesterol
actual <- original$Cholesterol[is.na(dat$Cholesterol)]
predicted <- imputed$Cholesterol[is.na(dat$Cholesterol)]
mean(actual)
[1] 231.07
mean(predicted)
[1] 223.4087
# Smoking
actual <- original$Smoking[is.na(dat$Smoking)]
predicted <- imputed$Smoking[is.na(dat$Smoking)]
table(actual)
No Yes
11 9
table(predicted)
No Yes
16 4
|
效果还行吧。Cholesterol 实际均值 231.07, 预测值为 223.4087;Smoking 缺失值里 15⁄20 预测是对的。
Amelia
Amelia 包前面就出现过了。我一般用 missmap 来迅速看一下数据里的缺失值的分布情况。
Amelia 这个名字来源于 Amelia Earhart,美国航空先驱、作家。她是世界上第一个独立飞行穿越大西洋的女飞行员。但在 1937 年一次环球飞行中,她在途径太平洋上空时神秘失踪(missing)了。所以这个专门用来处理 missing value 的包以 Amelia 命名。
Amelia 对缺失值假设为:
- 缺失值随机
- 数据中所有变量都满足多元正态分布(Multivariate Normal Distribution, MVN),可以使用均值和协方差来描述数据。
Amelia 利用 bootstrap,同样也是生成多组填补值。但相比 MICE,MVN 还是有一些局限:
- MICE 对缺失值的模拟是一个一个变量进行的,而 MVN 依赖整体数据的多元正态分布
- MICE 可以处理多种类型数据的缺失值,而 MVN 只能处理正态分布或经转换后近似正态分布的变量
- MICE 能在数据子集的基础上处理缺失值,MVN 则不能
Amelia 适合用于符合多元正态分布的数据。如果数据不符合条件,可能需要事先将数据转换为近似正态分布。
我们一样还用前面那个数据:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
library(mice)
set.seed(1234)
iris.mis <- missForest::prodNA(iris, noNA = 0.1)
amelia_fit <- amelia(iris.mis, m=5, parallel = "multicore", noms = "Species")
# 1 st of the rsults
head(amelia_fit$imputations$imp1)
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2000000 setosa
2 4.9 3.0 1.4 0.2000000 setosa
3 4.7 3.2 1.3 0.2000000 setosa
4 4.6 3.1 1.5 0.2000000 setosa
5 5.0 3.6 1.4 0.2000000 setosa
6 5.4 3.9 1.7 0.2200646 setosa
|
然后看看回归分析结果:
1
2
3
4
5
6
7
|
fit2 <- Zelig::zelig(Sepal.Width ~ Sepal.Length + Petal.Width, data = amelia_fit, model = "ls")
summary(fit2)
estimate std.error statistic df p.value
(Intercept) 1.8677059 0.36106651 5.172748 36.47085 8.567029e-06
Sepal.Length 0.3028491 0.07477405 4.050190 33.00981 2.560708e-04
Petal.Width -0.4761426 0.08182634 -5.818941 28.54299 1.160180e-06
|
均值或者中位值填补
在文献里可以大量看到直接用均值/中位值来填补缺失数据的。但这样做的前提应该也是数据里缺失值很少。
我在网上搜了几个办法:
How to fill NA with median?:
1
2
3
4
5
6
7
|
library(dplyr)
df %>%
mutate_all(~ifelse(is.na(.), median(., na.rm = TRUE), .))
# to replace a subset of columns:
df %>%
mutate_at(vars(value), ~ifelse(is.na(.), median(., na.rm = TRUE), .))
|
下面这个很重要:因为我们用均值/中位值填补 NA 只适用于连续型数据,而实际上数据往往是多种变量都有的,所以实际情况我们需要的往往是只对部分变量进行处理。
综合一下,我把上面的代码小小改动了一下,直接对变量进行筛选,遇到数值型变量就应用:
1
2
|
df %>%
mutate_if(., is.numeric, .funs = ~ifelse(is.na(.), median(., na.rm = TRUE), .))
|


